I quadrati ortogonali e ortodiagonali
di Massimo Gerardo CarreseNgurzu Edizioni, 2012 (fascicolo, pag. 25)
Paragrafi:– Un esempio performativo. Il quadrato ortogonale di Giuseppe Polone;
– Costruzione di un quadrato ortogonale 8×8 (con numeri a scelta, non progressivi);
– Lo spettatore protagonista. Costruire un quadrato ortogonale 8×8 con numero e posizione scelti dallo spettatore;
– Costruzione di un quadrato ortodiagonale 4×4 e 8×8 (con numeri a scelta, non progressivi) con valori indicati dallo spettatore;
– Bibliografia e Sitografia di riferimento.
Il testo descrive due tipologie di quadrati: ortogonali (la somma dei numeri in orizzontale ha una costante pari alla somma dei numeri in verticale; la somma dei valori della diagonale A è diversa da B) e ortodiagonali (più noto come “quadrato magico”, con costante uguale per tutte le possibilità spaziali: orizzontale, verticale, diagonale, simmetrico; a seconda del tipo di quadrati anche a zigzag, a scompartimento…).
Lo studio è un’introduzione ai quadrati (ortogonali e magici) e alle principali metodologie utili alla loro realizzazione. Molti gli esempi di schemi 4×4 e 8×8 con suggerimenti ludici, artistici e didattici dell’autore, come i quadrati ludici (il “quizquadrato”, termine con cui Carrese chiama i suoi schemi magici “a rompicapo” – un esempio con grado di difficoltà ‘semplice’ è riportato in basso), genetliaci (quadrati magici con data, mese e anno di nascita), artistici (ad esempio, quadrati magici incisi su pietre di fiume), didattici (il Gioco della Matematica nei quadrati ortogonali e ortodiagonali).
Il testo si chiude con esempi su come creare un quadrato magico e ortogonale, di matrice 4×4 e 8×8, coinvolgendo uno spettatore ideale a inserire in una casella qualsiasi un numero a sua scelta.
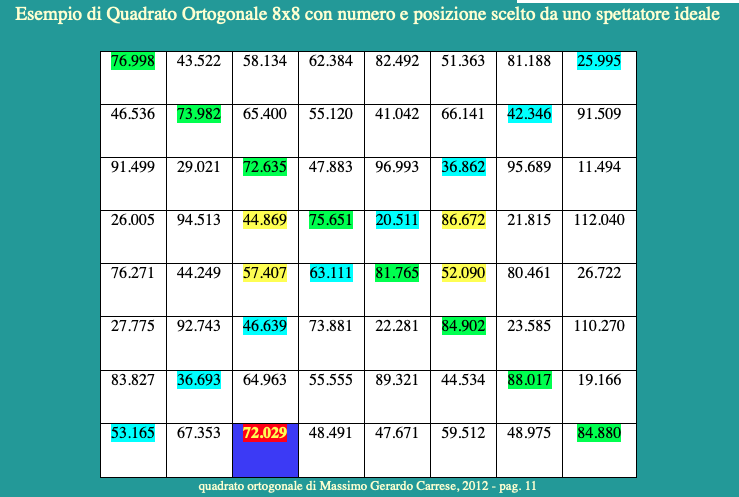
Il numero in rosso e la casella in blu sono scelti dallo spettatore: 72.029
Costante orizzontale e verticale = 482.076
Diagonale A (in verde) = 638.830
Diagonale B (in azzurro) = 325.322
La somma di quattro numeri simmetrici, presi casualmente all’interno del quadrato (come quelli evidenziati in giallo), è sempre pari alla metà della costante orizzontale e verticale = 241.038
Performance di un “quizquadrato magico”:
– il 14 ottobre 2012 è stato presentato un quizquadrato magico alla Libreria 80mq di Calvi Risorta (Caserta). Lo schema 4×4 in basso è stato realizzato appositamente da Carrese nell’ambito dell’incontro “Meraviglie del Gioco – aspetti ludici e didattici di giochi classici, fantasiologici, panassurdi, oplepiani”
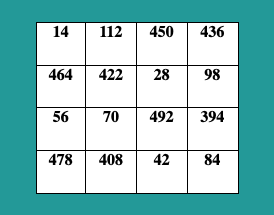
Il quizquadrato. Risolvi il Rompicapo.
Il quadrato magico si compone di tre elementi significativi, di cui uno in evidenza,
attinenti all’incontro tenutosi alla Libreria 80mq. Quali sono?
Nota: il problema è risolvibile anche da chi non era presente all’incontro…
grado complessità: semplice
invia la tua risposta a fantasiologo@fantasiologo.com

